Black Scholes Model

Before we move to different option greeks, let us learn a popular model called ‘The Black Scholes Model’ that is used to calculate option value.

The Black Scholes model, also known as the Black-Scholes-Merton (BSM) model, is a mathematical model for pricing an options contract. The Black-Scholes Merton (BSM) model is a differential equation used to solve for options prices. The model won the Nobel prize in economics. It's used to calculate the theoretical value of options using current stock prices, expected dividends, the option's strike price, expected interest rates, time to expiration and expected volatility.

The formula, developed by three economists—Fischer Black, Myron Scholes and Robert Merton—is perhaps the world's most well-known options pricing model.

The Black-Scholes model makes certain assumptions:

The option is European and can only be exercised at expiration.
No dividends are paid out during the life of the option.
Markets are efficient (i.e., market movements cannot be predicted).
There are no transaction costs in buying the option.
The risk-free rate and volatility of the underlying are known and constant.
The returns on the underlying asset are normally distributed.

While the original Black-Scholes model didn't consider the effects of dividends paid during the life of the option, the model is frequently adapted to account for dividends by determining the ex-dividend date value of the underlying stock.

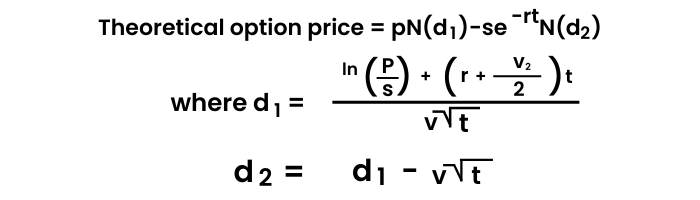
The variables are:

p= stock price
s= strike price
t= time to expiry
r= current risk-free interest rate
v= volatility measured by annual standard deviation
ln= natural logarithm
N(x)= cumulative normal density function